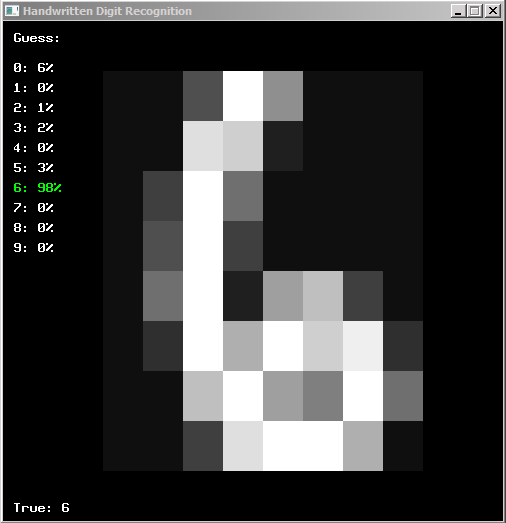
Here is a program that demonstrates using a neural network to recognize handwritten characters.
Not as verbose as my other entries as I wanted to keep it under 200 lines.
Written in BMaxNG.
You’ll need to download the training file here .
SuperStrict
Framework brl.basic
Import brl.glmax2d
Import brl.retro
Import brl.collections
AppTitle = "Handwritten Digit Recognition"
Graphics 500, 500
SeedRnd(MilliSecs())
Global x#[][]
Global y#[][]
LoadData()
Global NumBF% = 1 + Sqr(x.Length)
Global bf#[][] = New Float[NumBF][]
Global W#[,] = New Float[NumBF, 10]
Global Out#[] = New Float[10]
Global Sigma# = 2
Global rout#[Numbf]
Global err#
Global trainitr%
Global Kern#(a#[], b#[], s#) = RKernel 'RKernel 'IQuadKernel
'// INIT //
For Local i% = 0 Until NumBF
bf[i] = x[Rand(x.Length - 1)][..]
For Local j% = 0 Until 10
W[i, j] = Rnd(1 / Sqr(64)) * Sgn(Rnd(-1, 1))
Next
Next
While Not KeyHit(KEY_ESCAPE)
Cls
DrawData()
Local err# = (Train(x, y))
If(trainitr < 800) Then DrawText("Training" +[".", "..", "..."][trainitr Mod 3], 400, 10)
Flip
Wend
'----------------------------------------------------------------------------
Function Process%(in#[])
MemClear(VarPtr Out[0], Out.Length * SizeOf(1:Float))
For Local j% = 0 Until numBF
Local x# = kern(bf[j], in, Sigma)
For Local k% = 0 Until Out.Length
Out[k]:+(w[j, k] * x)
Next
rout[j] = x
Next
For Local k% = 0 Until Out.Length
Out[k] = sig(Out[k])
err:+Sqr((in[k] - Out[k]) ^ 2)
Next
End Function
'----------------------------------------------------------------------------
Function Train#(TData#[][], Targ#[][])
If trainitr > 800 Then Return 0
For Local i% = 0 Until TData.Length
err = 0
Local idx% = i
Local t#[] = targ[idx]
Process(TData[i])
For Local j% = 0 Until NumBF
For Local k% = 0 Until Out.Length
Local d# = (t[k] - Out[k])
w[j, k]:+(0.01 * d * rout[j])
Next
Next
Next
trainitr:+1
If trainitr < 300 Then lvq()
Return err
End Function
'----------------------------------------------------------------------------
Function lvq()
Local dat#[] = x[Rand(x.Length - 1)]
Local d# = 99999
Local b%
For Local i% = 0 Until bf.Length
Local td# = aDist(dat, bf[i])
If(td) < d Then
d = td
b = i
EndIf
Next
For Local i% = 0 Until bf[b].Length
bf[b][i]:+((0.1) * (dat[i] - bf[b][i]))
Next
End Function
'----------------------------------------------------------------------------
Function sig#(x#) Inline
Return 8.06356 / (0.422614 * x + 8.21913 / x + 16.2612 / (0.43677 * x + 7.87788 / x)) 't
End Function
'----------------------------------------------------------------------------
Function Normalize#(val#, desmin#, desmax#, natmin#, natmax#) Inline
Return desmin + (val-natmin)*(desmax-desmin)/(natmax-natmin)
End Function
'----------------------------------------------------------------------------
Function aDist:Float(v1:Float[], v2:Float[])
Local val:float = 0
For Local i:Int = 0 Until v1.Length
val:+((v1[i] - v2[i]) * (v1[i] - v2[i]))
Next
Return Sqr(val)
End Function
'----------------------------------------------------------------------------
Function IQuadKernel:Float(vA:Float[], vB:Float[], Sigma:Float)
Local prod#=0
For Local i% = 0 Until va.length
prod :+ ((va[i] - vb[i]) * (va[i] - vb[i]))
Next
prod = 1/(1+prod/(sigma*sigma)) 'Inv quad
Return prod
End Function
'----------------------------------------------------------------------------
Function RKernel:Float(vA:Float[], vB:Float[], Sigma:Float)
Local n#
For Local i% = 0 Until va.length
n:+(vA[i] - vB[i]) * (vA[i] - vB[i])
Next
Local d# = 2.0 * Sigma * Sigma
Local z# = n / d
Return Exp(-z)
End Function
'----------------------------------------------------------------------------
Function DrawData()
Local t% = Max(0, Abs(MilliSecs() / 3000))
Local i% = t Mod x.Length - 1
SetColor 255, 255, 255
Local Count%
Local c#
For Local yy# = 0 Until 8
For Local xx# = 0 Until 8
c = Normalize(x[i][Count], 0, 255, -1, 1)
SetColor(c, c, c)
DrawRect(100 + xx * 40, 50 + yy * 50, 40, 50)
Count:+1
Next
Next
SetColor 255, 255, 255
For Local j% = 0 Until y[i].Length
If y[i][j] > 0.5 Then DrawText("True: " + j, 10, 480)
Next
Process(x[i])
Local hi%, hv# = -999
Local tn%
For Local j% = 0 Until 10
If Out[j] > hv Then hi = j;hv = Out[j]
If y[i][j] > 0.5 Then tn = j
Next
For Local j% = 0 Until 10
SetColor 255, 255, 255
If j = hi And hi <> tn Then SetColor 255, 0, 0 'Else SetColor 255, 255, 255
If j = hi Then SetColor 0, 255, 0 Else SetColor 255, 255, 255
DrawText(j + ": " + Int(Max(Out[j], 0) * 100) + "%", 10, 40 + (j * 20))
Next
DrawText("Guess:", 10, 10)
End Function
'----------------------------------------------------------------------------
Function LoadData()
Local dlist:TLinkedList < Float[] >= New TLinkedList < Float[] > ()
Local ylist:TLinkedList < Float[] >= New TLinkedList < Float[] > ()
Local F$ = LoadText("optdigits.tra")
If Trim(F).Length = 0 Then RuntimeError("Oops!")
Local line$[] = f.split("~n")
For Local i% = 0 Until line.length
If Rnd(0,1)>0.3 Then Continue
Local aline$[] = LINE[i].Split(",")
Local tmpy#[10]
tmpy[Int(aline[64]) ] = 1
Local tmpX#[64]
For Local j% = 0 Until 64
tmpX[j] = (Float(aline[j]) - 7) / 8
Next
dlist.AddLast(tmpX)
ylist.AddLast(tmpy)
Next
x = dlist.ToArray()
y = ylist.ToArray()
End Function